|
Kernbegrippen van het lesmateriaal Een van de belangrijke taken van de leraar is om in de les de begrippen die er toe doen extra nadruk te geven en te blijven geven. Begrippen die steeds terugkomen in de les, begrippen die leerlingen structuur geven. Het lesmateriaal is behoorlijk omvangrijk. Wij willen een paar punten van de gekozen didactiek naar voren brengen zodat je meer grip krijgt op het materiaal. Er is heel veel literatuur beschikbaar. Statistiek is waarschijnlijk het meest onderwezen vak op de universiteit. En op middelbare scholen over de hele wereld wordt statistiek ook steeds meer onderwezen. Wij hebben daarom wat literatuur verzameld waaruit je inspiratie kunt opdoen. Inhoudelijke kernbegrippen De rol van toeval. Bijna iedere volwassene is ervan overtuigd dat het toeval een grote rol speelt in zijn leven en bij wat er in de maatschappij gebeurt. In waarnemingen zit vaak een zekere mate van variabiliteit. Het is zaak om dat inzicht regelmatig te herhalen, zodat leerlingen gevoeliger worden voor de variabiliteit van data. Toeval in de greep. Zodra je voldoende data hebt van goede kwaliteit, kun je iets gaan zeggen over kansen. In deze cursus leren leerlingen te beoordelen hoeveel gegevens daarvoor voldoende zijn. Formele kansrekening komt niet aan de orde. Het kansbegrip zit verweven in de (gesimuleerde) kansverdeling, met de variabiliteit als belangrijk kenmerk. We zitten daarmee goed in de internationale trend van het statistiek onderwijs. Verschil steekproef-populatie. Het doel van de statistiek is om op grond van een steekproef iets te zeggen over een populatie. Onderstaande plaatje speelt daarin een grote rol. 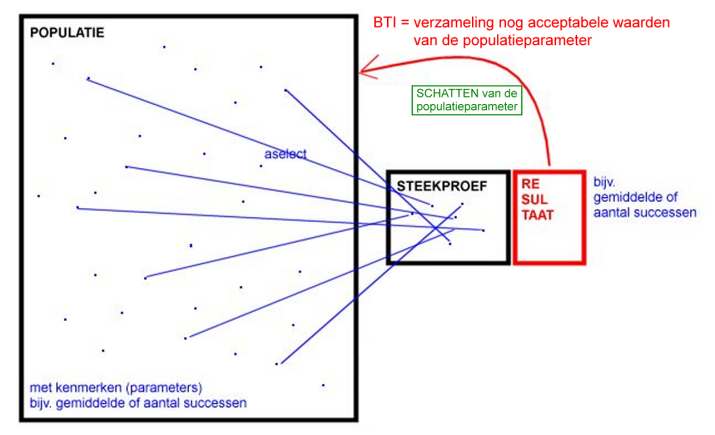 Goede kwaliteit data. Data van goede kwaliteit krijg je door een gerandomiseerd dubbelblind experiment op te zetten. Pas dan kun je iets "statistisch bewijzen". Het is vaak lastig om de populatie waarvoor de uitspraak geldt goed te beschrijven. Resampling methode. Er zijn verschillende resampling methoden. Wij gebruiken vooral de bootstrap. Dat wil zeggen dat je door herhaald te trekken (met teruglegging) uit de echte waarnemingen een betrouwbaarheidsinterval kunt aangeven voor bijvoorbeeld het gemiddelde van de populatie waaruit de steekproef is getrokken. Aangetoond is dat je in een groot aantal gevallen deze methode kunt toepassen (zie de app "Het bootstrap principe"). Het gaat steeds op een vergelijkbare manier in andere omstandigheden. Het grote didactische voordeel is dat de leerling bijna niet hoeft te worden geconfronteerd met kansrekening of formules die uit de lucht vallen. Op deze manier kan hij in het vwo eerst vertrouwd raken met begrippen als betrouwbaarheidsinterval en het toetsen van een hypothese. Later op de universiteit kan zij dan indien nodig de meer parametrische aanpak leren. De ervaring van de afgelopen jaren is dat dit bij deze leerlingen opvallend gemakkelijk gaat. Didactische aanpak Het is natuurlijk echt nodig dat je als leraar zelf een goed inzicht hebt in de aanpak. Concentrische aanpak. Statistiek is een onderwerp waar leerlingen lastig grip op kunnen krijgen. Dus gun ze de tijd om te rijpen. Er zit daarom ook behoorlijk wat herhaling in het materiaal.
In traditioneel statistiek onderwijs is sprake van vaak onbegrepen regels en formules die toegepast moeten worden. Maar ook met de aanpak die in dit lesmateriaal gekozen is, moet je goed opletten dat leerlingen steeds begrijpen wat er gebeurt. Dus niet klakkeloos een paar keer op de 1000-knop drukken en het interval aflezen van het scherm. Het blijft heel belangrijk om steeds het simuleren ook op de langzame manier te laten doen en de leerlingen te laten uitleggen wat er gebeurt. Een aardige opdracht aan de leerlingen: leg aan een niet al te dom familielid uit wat er gebeurt in de simulaties, of wat een begrip zoals betrouwbaarheidsinterval inhoudt. Inspirerende Literatuur Een hele goede bron is de blog van Allan Rossman https://askgoodquestions.blog/ Hij heeft intussen 100 blogs over statistiek onderwijs gepubliceerd. Het zijn blogs waaruit je inspiratie kunt opdoen voor je les, maar ze leveren ook veel vragen en thema's waaraan je je eigen kennis als leraar kunt toetsen. In Toeval in de greep is gebruik gemaakt van een aantal suggesties uit deze blog. In Nieuw Zeeland bestaat een heel actieve groep statistiek docenten. Belangrijke namen daarbij zijn Chris Wild en Maxime Pfannkuch. Ook de blog van Anna-Marie Fergusson geeft interessante informatie. https://teaching.statistics-is-awesome.org/home/ Ook in de VS zijn er grootse plannen met het statistiek onderwijs. Hierbij een link naar het complete GAISE rapport. Hun plannen gaan behoorlijk ver. Wel zijn er problemen met de deskundigheid van leraren. https://www.amstat.org/asa/files/pdfs/GAISE/GAISEPreK-12_Full.pdf Voor de lerarenopleiding is er het set-rapport dat allerlei suggesties geeft om leraren en onderwijzers goed voor te bereiden op modern statistiek onderwijs. https://www.amstat.org/asa/files/pdfs/edu-set.pdf Tijdschrift: Statistics Teacher www.statisticsteacher.org Een voorbeeld van een modern statistiek boek met een mengsel van apps, video's en teksten is Artofstat. http://artofstat.com Het boek "Storytelling with data" van Cole Nussbaumer Knaflic was onze inspiratie voor hoofdstuk 5C van deel 0. De video https://youtu.be/8EMW7io4rSI is een video van Cole's presentatie aan haar oud-collega's van Google. |
Artikel in Euclides |