9C. Uitwerkingen.

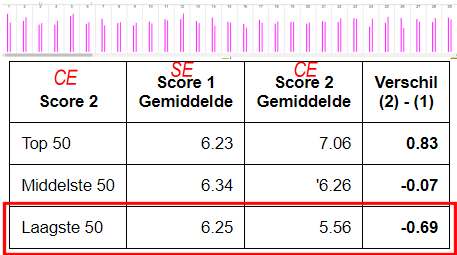
Opgave 1.

SE: Schoolexamen (PTA); CE: Centraal (landelijk) examen.

- Bas: SE: 6,3-0,5=5,8 en CE: 6,3-0,7=5,6
Piet: SE: 6,3+1,0=7,3 en CE: 6,3+1,4=7,7

- Voor scholen met veel Bassen is dus het CE lager dan het SE en voor scholen met veel Pieten is
het CE hoger dan het SE.

- Het is dus louter een gevolg van het feit dat de variabiliteit van het SE groter is dan die van het CE!
De oorzaak hoeft niet te liggen in een gewoonte van scholen met veel zwakke leerlingen om het SE te
hoog te scoren in hun beoordeling. Het is een statistisch verschijnsel, en geen oorzakelijk verschijnsel.

- Daar zal naar statistsche verwachting het CE juist hoger zijn dan het SE.

Opgave 2.

- De staafjes tonen dus steeds een tweetal cijfers
van een leerling; eerst het SE dan het CE.
Er zijn 150 leerlingen gesimuleerd, in de
veronderstelling dat ze helemaal dezelfde
normale kansverdeling hebben voor hun
SE-cijfer en hun CE-cijfer.

De onderste rij van de tabel laat nu ongeveer het
volgende zien: de 50 zwakste leerlingen scoren op
hun SE gemiddeld 0,7 punt hoger dan op hun CE.

- Het is een statistisch verschijnsel, en geen oorzakelijk verschijnsel, want de verdelingen van de SE-cijfers
en de CE-cijfers waren gelijk. Maar als je alleen let op de scholen met veel leerlingen met lage CE-cijfers
(onderste rij), dan kun je dus alleen al door de statistiek verwachten dat hun SE-cijfers gemiddeld hoger
zijn dan hun CE-cijfers.

Opgave 4.

- Je ziet dat steeds het IQ van de ouders gemiddeld dichter bij de 100 ligt dan het IQ van het kind.
(Dat zal trouwens andersom ook het geval zijn: het IQ van de kinderen ligt gemiddeld dichter bij
de 100 dan het IQ van de moeder of vader)

- IQ=70; afwijking van midden is 30; 60% daarvan is 18; gemiddeld IQ ouders is dus 100-18=82.
- 88; 118; 100; 130.

- Ouders hebben een normale verdeling met μ = 118 en σ = 12; ga naar de app "Verdelingen" en zorg
dat je deze normale verdeling ziet; schuif nu rechts naar 130, en je vindt 16%.
- Ouders hebben een normale verdeling met μ = 118 en σ = 12; ga naar de app "Verdelingen" en zorg
dat je deze normale verdeling ziet; schuif nu links naar 130, en je vindt 69%.

- Als de genen/omgeving/opvoeding helemaal geen invloed zouden hebben, dan krijg je toch een zekere
regressie naar het midden. Het experiment met het gooien van muntstukken (opgave 3) toont dat aan.
Ook de redenering en de app in opgave 2 toont dat aan (we veronderstelden daar dat SE en CE dezelfde
verdeling hebben, immers).
Maar als de genen ook effect zouden hebben, dan krijg je toch nog het waargenomen effect, zij het in
wat mindere mate.