7E. Uitwerkingen.

Opgave 1.

Als je de temperatuur constant houdt en je kijkt naar de correlatie tussen Polio en Frisdrank, dan zie je bij elke temperatuur dat het plaatje eigenlijk geen correlatie vertoont.
Als je kijkt naar de temperatuur en Polio, dan is er een sterke positieve correlatie, en dat is ook zo bij temperatuur en Frisdrank. De temperatuur is dus een derde factor, die zowel Polio als Frisdrank positief beïnvloedt. Daardoor lijkt er een sterk verband te zijn tussen Polio en Frisdrank, maar dat is er dus niet. Het is dus voorbeeld A.

Opgave 2.

a.
Een niet-aselecte steekproef: men bekijkt alleen topsporters. Dit geldt dus alleen voor topsporters (en bovendien staat er ook niets over de voorwaarde dat de steekproef aselect moet zijn getrokken uit alle topsporters). Het is voorbeeld C.
b.
Voorbeeld D. Hier worden verschillende deelpopulaties op één hoop gegooid. Mannen drinken meer bier en vrouwen gebruiken meer make-up. Je kunt ook zeggen: er is een derde factor, namelijk geslacht.
c.
Vertraging: de reclame werkt niet meteen; mensen gaan later misschien meer kopen omdat ze de reclame hebben gezien. Voorbeeld E.

Opgave 3.

Invullen in de lijsten van de GRM. Een zwak verband (zie overzicht in hoofdstuk 7A)

Opgave 4.

Ongeveer twee maanden, zo te zien.

Nieuwe tabel:

correlatie r = 0,65
Type uit voorbeeld E : Vertraging.

Opgave 5.

Het punt (2,10) is een uitschieter.
MET (2,10) is de correlatiecoëfficiënt gelijk aan r = 0,043
ZONDER (2,10) is de correlatiecoëfficiënt gelijk aan r = 0,849

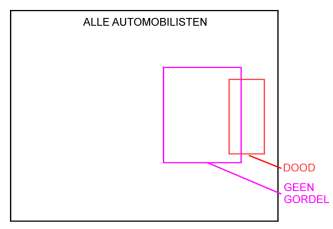
Opgave 6.

a. derde factor leeftijd.
b. invloed van het seizoen: tulpenbollen koop je in december.
c. invloed van de luchtdruk: op grotere hoogte is de luchtdruk lager en de luchtweerstand dus ook lager;
ook smelt het ijs onder druk van de schaatser makkelijker.
d. derde factor: geldelijk vermogen
e. derde factor: Bruto Nationaal Inkomen
f. als een goed geneesmiddel sterfte aan een bepaalde ziekte vermindert, dan wordt vanzelf de sterfte aan
andere ziektes groter; je moet érgens aan dood gaan .....

Opgave 7.

Als A groter wordt dan wordt B kleiner (negatieve correlatie).
En als B kleiner wordt dan wordt C ook kleiner (positieve correlatie).
Dus: als A groter wordt dan wordt C kleiner, en dat is een negatieve correlatie.

Opgave 8.

a. Ouderen hebben meer rollators nodig.
b. Niet-mobiele mensen laten de pizza thuis bezorgen.
c. Wie met hoge rapportcijfers thuiskomt wordt beloond met taart.
d. Wie ADHD heeft gaat meer snoepen.
e. Hogere inkomens sporten meer.
f. Intelligente mensen lezen meer.

Opgave 9.

Kijk maar naar dit plaatje:

Opgave 10.

- r = 0,885
- positieve correlatie; zeer sterk.
- vink "Bootstrap" aan, en je vindt een 95%-BTI voor r tussen 0,85 en 0,91
- vul rechtsboven waarde = 2 in; vink "Betrouwbaarheidsinterval" aan; simuleer;
je vindt een gemiddelde wachttijd tussen 54 en 57 minuten.
- er wordt steeds een nieuwe bootstrap-steekproef gemaakt uit de waargenomen steekproef;
telkens wordt de trendlijn (regressielijn) bepaald en daarmee wordt de y-waarde die hoort bij x = 2
berekend. Deze y-waarden worden in de onderste laag geturfd.
Zo ontstaat het BTI voor de gemiddelde waarde die hoort bij x = 2 in de populatie.
- bij x = 3 hoort het BTI van 65 tot 67 minuten; bij x = 4 hoort het BTI van 76 tot 77 minuten.

Opgave 11.

- r = 0,578
- positieve correlatie; matig.
- 95%-BTI voor r tussen 0,41 en 0,71
- BTI voor gemiddeld cijfer EN in de populatie: tussen 5,8 en 6,2
- terug naar Data analyse; weer naar Resampling regressie met MAAT en NE;
bij x = 7,5 hoort een BTI voor het gemiddeld cijfer NE in de populatie: tussen 6,5 en 6,8
- tussen 6,7 en 7,3.

Opgave 12.

- r = -0,695
- negatieve correlatie; matig tot sterk.
- x = 50: 95%-BTI gemiddelde levensverwachting 13 tot 20 jaar.
(mits de steekproef goed aselect was)
- x = 100: 12 tot 17,5 jaar; x = 250: 7 tot 12 jaar; x = 500: 0 tot 5 jaar.

Opgave 13.

- r = -0,776
- negatieve correlatie; sterk; eigenlijk een sterke positieve correlatie tussen de prestaties!
- x = 10,5: 95%-BTI gemiddelde sprongafstand in de populatie: tussen 230 en 260 cm.
(mits de steekproef goed aselect was)
- terug naar Data analyse; nu volgorde sprong en sprint omkeren;
x = 400: 95%-BTI gemiddelde sprint in de populatie: tussen 7,7 en 8,2 sec.

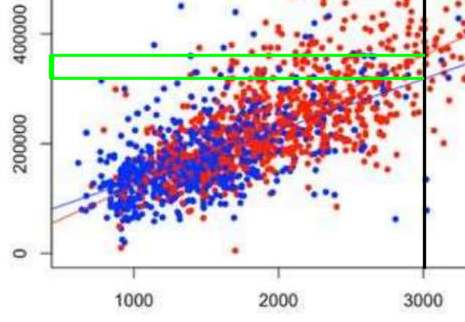
Opgave 14.

- r = -0,888
- negatieve correlatie; zeer sterk.
- x = 100000: 95%-BTI gemiddelde prijs tussen 12500 en 14500.
(mits de steekproef goed aselect was)

Opgave 16.

- jongens: r = 0,64; meisjes: r = 0,45; bij meisjes dus meer spreiding in de puntenwolk.
- 95%-BTI jongens voor r tussen 0,49 en 0,76, voor meisjes tussen 0,28 en 0,62; overlap: 0,49 tot 0,62.
schuiven in de bootstrapverdeling van de jongens levert ongeveer 100-2,5-64,5 = 33%.

JONGENS:
- r = 0,55; matig positieve correlatie.
- wisk = 3 geeft een 95%-BTI voor het gemiddelde schoolcijfer in de populatie tussen 5,1 en 6,1.
MEISJES:
- r = 0,61; matig positieve correlatie; nauwelijks anders dan bij de jongens.
- wisk = 3 geeft een 95%-BTI voor het gemiddelde schoolcijfer in de populatie tussen 5,5 en 6,4.

Opgave 17.

Kijk maar naar dit plaatje:
Het verschil tussen de trenslijnen
bij x = 3000
is ongveer 4000 $.

Opgave 18.

1-D ; 2-B ; 3-A ; 4-C