5C. Uitwerkingen.

Opgave 1. Sporttraining.

a. Onderzoeksvraag: Scoort haar groepje beter dan het NL gemiddelde?
De toevalsvariabele is de geworpen afstand. Type kwantitatief meetgegeven.
Nulhypothese: Haar groepje is niet beter. D.w.z:
H₀: populatie is normaal met μ = 62,0 en σ = 6,0.
Alternatieve hypothese: Haar groepje is wel beter. Dus H₁: μ > 62,0.
De populatie is de denkbeeldige verzameling van eindeloos veel worpen die haar
groepje vandaag zou kunnen gooien.
De steekproefgrootheid is het gemiddelde van de waarnemingen van de steekproef.
Stel de app "Steekproevenverdeling" in op μ = 62,0 en σ = 6,0.
Stel de omvang van de steekproef in op n = 45.
Gebruik de simulatie-app om het 99%-kritieke gebied te bepalen.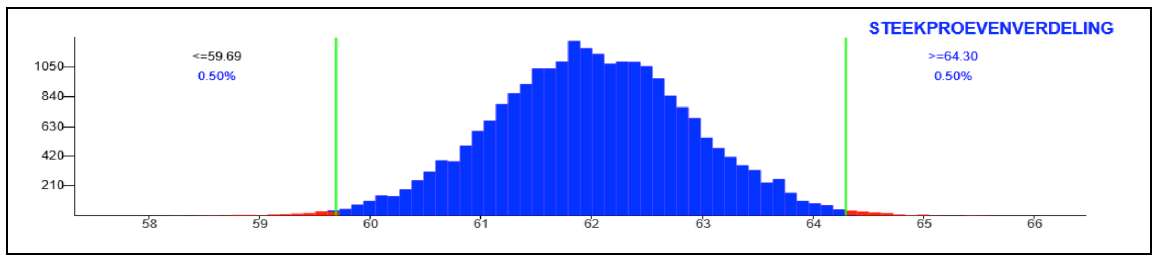

De waargenomen waarde van de steekproefgrootheid (64,4) ligt IN het kritieke gebied.
Er is dus voldoende aanleiding om te beweren dat de training heeft geholpen.
b. Deze groep speerwerpsters is geen aselect gekozen steekproef uit alle speerwerpsters van 18 jaar en
ouder. Dus je kunt de conclusie dat de training helpt niet zomaar veralgemeniseren.
Daartoe zou je een aselect gekozen steekproef uit alle R'damse speerwerpsters moeten nemen.

Opgave 2. Sporttraining.

a. Als de steekproefomvang minder wordt, wordt de invloed van het toeval groter.
De ongeveer normale steekproevenverdeling in de onderste laag wordt dan breder (de SD wordt immers
groter). Dus wordt het 99%-binnen-gebied ook groter, en het kritieke gebied wordt daarom kleiner.
b. Met de app zie je dat bij n = 25 de waargenomen waarde van de steekproefgrootheid (64,4) niet meer
IN het kritieke gebied ligt.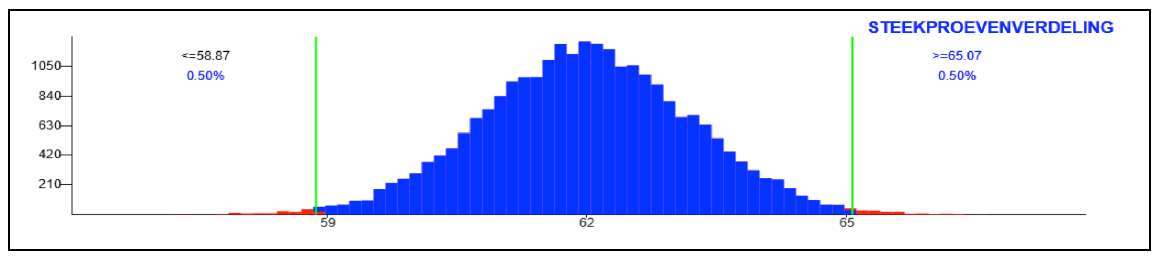

Het testresultaat is nu niet meer significant bij een gemiddelde van 64,4 meter.
c. Aan het plaatje zie je dat het steekproefgemiddelde dan 65,1 meter had moeten zijn.

Opgave 3. Speerwerpen.

a. Goede aselecte steekproef uit de populatie van alle speerwerpsters in NL.
De snelle methode voor het 95%-BTI: zet de populatie op μ = 61,4 en & = 5,8.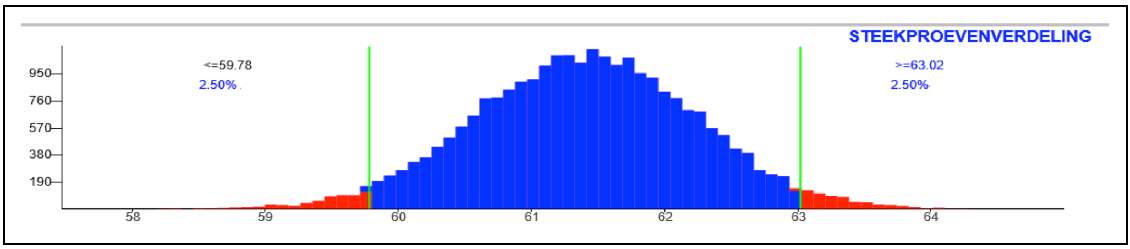

Maak een steekproevenverdeling (bij n = 50) en gebruik de 95%-knop.
Het 95%-BTI is dan het interval tussen 59,8 en 63,0 meter.
b. Betekenis:
- het is de verzameling nog aannemelijke waarden van de populatie-μ bij een significantiedrempel
van 2,5%. Als je deze waarden als nulhypothese zou testen met dit waargenomen steekproef-
resultaat, dan zou je de nulhypothese niet verwerpen.
- er is 95% kans dat jouw BTI de werkelijke populatieparameter bevat.
c. Nu wordt de steekproefomvang 2 keer zo groot. Dan wordt het toeval √2 keer zoveel teruggedrongen.
Het 95%-BTI wordt dus smaller rondom 61,4, en wel √2 keer zo smal.

Opgave4. Vuisthoogte.

a. H₀: geen verschil in vuisthoogte tussen oude en jonge mannen, dus vuisthoogte oude mannen is normaal verdeeld met gemiddeld 817 mm en standaardafwijking 47 mm.
H₁: wel verschil in vuisthoogte tussen oude en jonge mannen, dus vuisthoogte oude mannen is gemiddeld kleiner dan 817 mm.
n = 128 (steekproefomvang)
X = waargenomen waarde: het steekproefgemiddelde is 761.
Simuleer met app Steekproevenverdelingen. Bepaal het 95%-kritieke gebied.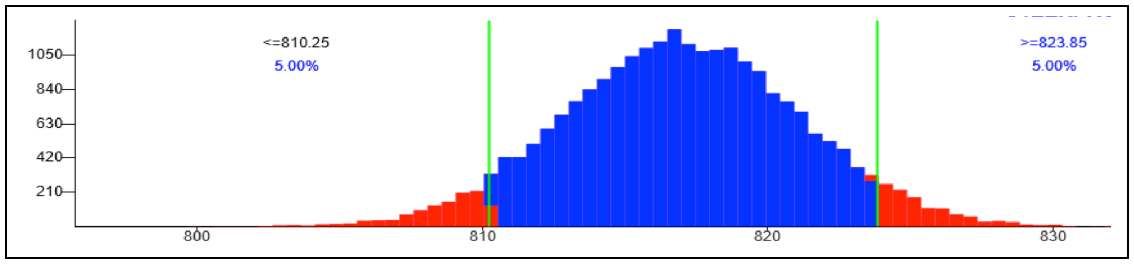

De waargenomen waarde van het steekproefgemiddelde (761) ligt links in het kritieke gebied.
Er is voldoende aanleiding om te stellen dat de vuisthoogte van oudere mannen korter is.
b. Je ziet bovendien dat je pas bij een waarneming van het steekproefgemiddelde van minstens 810
buiten het kritieke gebied bent gekomen. Pas dán vind je H₀ nog aannemelijk.