1B. Opdrachten over de Sportprestaties.

Deze opdrachten doen jullie in een groepje. De leraar deelt de groepjes in. De leraar zegt over welke opdrachten het weekverslag moet gaan. Elk groepje maakt een mooi verslag in Google Docs. Daarin staan tekst EN plaatjes. Die laten zien hoe je het antwoord op de opgaven hebt gevonden. Zorg er wel voor dat ALLE blauwe vragen in je verslag beantwoord worden. De leraar kan jullie vragen om dat verslag als een presentatie aan de klas te tonen.

Opgave 1. Video kijken en gegevensbestand inladen. In DEZE VIDEO's wordt voorgedaan hoe je met dit gegevensbestand kunt werken. Video 1 (Bestand openen in VUStat) Video 2 (Dotplot en Boxplot) Video 3 (Tabel en Histogram) a. Bekijk ze nu, en bekijk ze later misschien nog eens als je dat handig vindt. In Hoofdstuk 1A staat alles kort samengevat. b. Laad nu het gegevensbestand "sport" in je computer. In hoofdtuk 1A is voorgedaan hoe dat moet.

Opgave 2. Op volgorde zetten. Als je bovenaan een kolom op de naam van de variabele klikt, dan wordt het bestand gesorteerd op de volgorde van die kolom. Nog een keer klikken: de volgorde wordt omgekeerd. Gebruik deze truc bij de volgende vragen. a. Er was iemand heel langzaam op de sprint, en tegelijk ook heel slecht op vérspringen en     vérgooien. Is het een jongen of een meisje? Hoe oud is hij/ze? Welk rugnummer?     Schrijf ook op hoe je daar snel achter bent gekomen.     Misschien was dit kind op die dag wel ziek. b. Wie was het best in vérspringen? Jongen of meisje? Hoe oud? Rugnummer?     Was die ook het best in vérgooien? c. Wat is het verschil in cm tussen de verste sprong en de minst verre sprong? d. Hoeveel kinderen liepen de sprint in minder dan 9 seconden? e. Wat is het verschil in cm tussen de verste gooi en de minst verre gooi, als je dat zieke kind niet     meetelt?

Opgave 3. De Dotplot en de Boxplot. a. Wijs Grafiek aan en kies Dotplot. Kies de variabele "Vérspringen".     Klik ook het hokje van Grote straal aan (dat noem ik "aanvinken").     Hoeveel bolletjes zie je? Wat betekent elk bolletje? b.Vink nu ook het hokje van Boxplot aan.     Hoeveel procent van alle bolletjes zit in het gele gebied?     Wat zijn de waarden van het eerste kwartiel, de mediaan en het derde kwartiel?     (Gebruik het laatste plaatje in hoofdstuk 1A voor de vorige vraag)     Bedenk een andere naam voor de mediaan, waar het woord "kwartiel" in zit.     Vul aan: "50% van alle bolletjes ligt links van de ........, en 50% ligt er rechts van".     Wat gebeurt er met de boxplot als je de "Uitschieters" aanvinkt? c. Klik nu Groeperen aan, en kies de variabele "Geslacht".     Vink het rondje aan van . Dan zie je de plaatjes van jongens en meisjes.     Schrijf nu op waaarin meisjes en jongens verschillen als je op vérspringen let;     noem zoveel verschillen als je kunt ontdekken.

Opgave 4. Het Histogram en de Kengetallen. a. Vink nu ook het hokje van Histogram aan.     Je ziet hier het histogram van de mannen. We noemen zoiets ook wel een staafdiagram.         De bolletjes zijn ingedeeld in klassen. Er zijn 10 klassen gemaakt.     Wat is de klassenbreedte die door de app is gemaakt?     Hoe bepaalt de app de hoogte van elk staafje?     Zo'n plaatje toont de verdeling van de waargenomen waarden van de variabele vérspringen.     Kun je misschien nog meer verschillen opschrijven tussen de twee verdelingen van de jongens en     van de meisjes dan in opgave 3c? b. Klik nu op Kengetallen     Waren er meer meisjes dan jongens?     Hoeveel cm sprongen de jongens gemiddeld verder dan de meisjes?     Kloppen de waarden van de medianen ongeveer met wat je opschreef in opgave 3? c. Sluit nu eerst de Kengetallen en haal het vinkje bij het Histogram weer     weg voor je verder gaat.     Kies nu een andere variabele, namelijk Sprint (helemaal rechts boven).     Wat vind je van het verschil tussen meisjes en jongens op de sprint?     En wat vind je van het verschil tussen jongens en meisjes bij het vérgooien?     Je kunt natuurlijk ook de kengetallen gebruiken in je antwoordverslag..... d. Hef nu de groepering naar geslacht weer op . Sluit tenslotte de Grafiek     Nu ben je weer terug bij het gegevensbestand zelf.

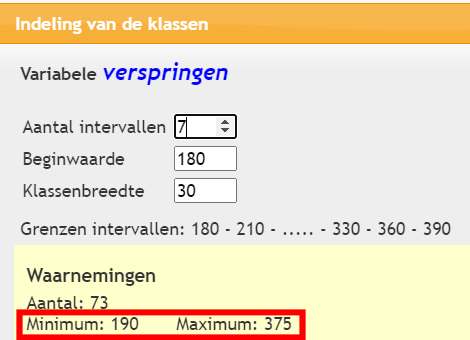
Opgave 5. Klassenbreedte. a. Wijs Grafiek aan en kies Histogram. Kies de variabele "Vérspringen".    Klik op "Indeling". En dan zie je dit:    Onderaan dat plaatje staat dat de waarden    beginnen met 190 en eindigen met 375.    De totale breedte is dus ongeveer 200.    De app heeft bedacht dat er dan 7 klassen    met breedte 30 moeten komen.    Dat kan natuurlijk ook anders:    10x20 of 5x40 of 2x100 of 20x10 of 40x5 0f 200x1.    We gaan hierme experimenteren.    Zet het aantal intervallen op 10, en zet daarna de Beginwaarde op 190, en zet    de klassenbreedte op 20; check nog even goed of de app niet tóch weer eigen    bedachte waarden heeft ingevuld voordat je op OK drukt. Bekijk het plaatje. b. Doe dit telkens voor alle hierboven genoemde klassenbreedtes en schrijf een verslagje     over wat je aan de verschillende histogrammen ziet veranderen.     Schrijf er bij welke klassenbreedte volgens jou het beste overzicht over de waarnemingen     geeft. Zet er ook bij waaróm je dat vindt. Je kunt het zó formuleren:     Een dotplot (klassenbreedte = 1) toont gegevens (data) en een histogram geeft (meer of minder) informatie afhankelijk van de klassenbreedte.

Opgave 6. Kansen. a. Begin weer met het maken van een histogram van "vérspringen".    Zet de indeling op aantal intervallen = 10, Beginwaarde = 190,    klassenbreedte = 20;    check nog even goed of de app niet tóch weer eigen bedachte waarden heeft ingevuld voordat    je op OK drukt.    De hoogte van de staafjes geven de aantallen kinderen in de betrokken klassen.    Die aantallen noemen we ook wel de frequenties.    Je kunt er ook percentages van laten maken. Vink "Percentages" aan.    Die percentage noemen we ook wel de relatieve frequenties.    Vink nu "Schuiven" aan. Je ziet twee groene lijnen. Die kun je schuiven.    Bedenk hoe je kunt laten zien dat de kans dat een willekeurig kind verder springt    dan 3,50 meter gelijk is aan 9,59%. b. Nu gaan we schuiven in de Dotplot. Dat is nauwkeuriger.     Sluit het histogram. Start de Dotplot, weer van "Vérspringen". Ook daar kun je Schuiven.     Voor de mediaan geldt: 50% van de kinderen springt verder.     Zoek de mediaan met de hulp van "Schuiven" en controleer bij de Kengetallen of dat klopt.     Wat is de kans dat een willekeurig kind minder dan 3 meter springt?     Wat is de kans dat een kind tussen 300 en 330 cm springt?     Is de verdeling redelijk symmetrisch rondom de mediaan?     Onderzoek dat, door van de mediaan 40 cm naar rechts en 40 cm naar links te gaan.     Is de verdeling misschien redelijk symmetrisch rondom het gemiddelde?     Beschrijf wat de computer doet, volgens jou, om die kansen uit te rekenen.

Opgave 7. Verschil tussen de groep van elf- en de groep van twaalf-jarigen? a. Onderzoek het verschil tussen deze twee groepen op de drie variabelen     Sprint, Vérspringen en Vérgooien; schrijf een uitgebreid verslag van je bevindingen.

Opgave 8. Lijndiagram (frequentie-polygoon). Zorg dat je alles waar je mee bezig was weer sluit. Je bent nu weer terug bij het gegevensbestand zelf. Wijs Grafiek aan en kies Lijdiagram. Kies de variabele "Vérspringen". Als het goed is staat de indeling nog steeds op: aantal intervallen = 10, Beginwaarde = 190, klassenbreedte = 20 a. Als dat niet zo is, zorg dan voor deze indeling.     Zorg dat je de percentages te zien krijgt; dan heb je een "relatief frequentie polygoon".     Het lijndiagram loopt van punt tot punt. Wat hebben die punten met het histogram te maken?     Let op hun hoogte (y-coördinaat) en op hun ligging (x-coördinaat). b. Vink nu het hokje"cumulatief aan, en beschrijf hoe deze figuur gemaakt is door de app.     Deze figuur heet een cumulatief relatief frequentie polygoon     Wat denk je dat het woord "cumulatief" in gewoon Nederlands betekent? c. In het cumulatief relatief frequentie polygoon kun je bij de mediaan een vertikale lijn omhoog     trekken. En daarna de horizontale lijn naar links. 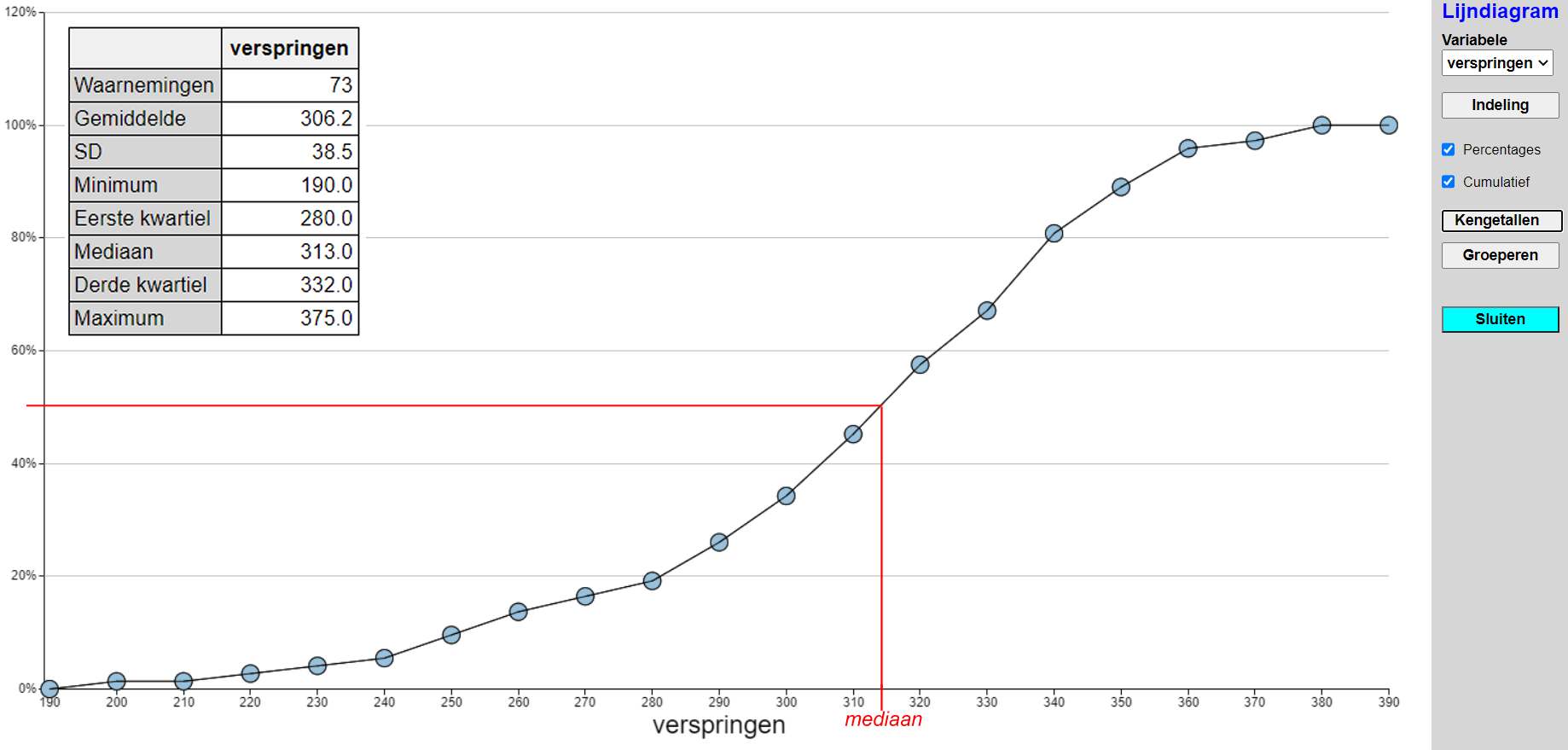    Bij welk percentage moet die horizontale lijn ongeveer uitkomen op de y-as?     Leg in je verslag uit waarom dat zo moet zijn, en waarom dat ongeveer zo moet zijn.

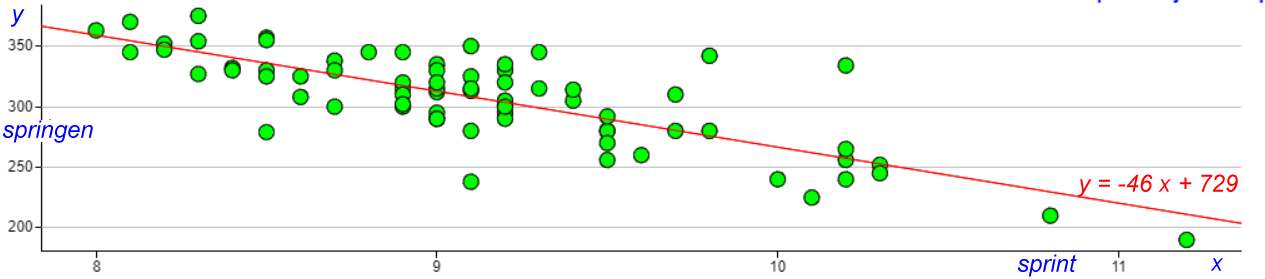
Opgave 9. Puntenwolk. Zorg dat je alles waar je mee bezig was weer sluit. Je bent terug bij het gegevensbestand zelf. Wijs Resampling aan en kies Resampling regressie. Kies de twee variabelen "Sprint" en "Vérspringen". Je wordt doorgestuurd naar een nieuwe app die de puntenwolk laat zien. Start die app. Nu zie je het statistisch verband tussen die twee variabelen. De app heeft zo goed mogelijk een rechte lijn getekend, die het beste past bij die puntenwolk. Een soort trendlijn. De formule voor die lijn staat erbij. a. Bereken je beste voorspelling van de sprong van een kind dat 50 meter in 10,5 seconden liep. Een manier om de sterkte van het statistisch verband aan te geven, is met de correlatiecoëfficiënt r. Die meet, ruw gezegd, hoeveel de gezamenlijke punten van de wolk afwijken van de trendlijn. De app berekent de waarde van r. Die staat rechts boven de puntenwolk. Daar staan ook de a en de b van de formule voor de trendlijn: y = ax + b. Als r = 1 dan liggen alle punten op de lijn. Dan is er geen wolk. Als r=-1 is dat ook het geval. Maar als r=1 dan loopt de lijn schuin omhoog, en bij r=-1 schuin naar beneden. Als de trendlijn schuin omhoog loopt, dan is er een positieve correlatie. Als de trendlijn schuin naar beneden loopt, dan is er een negatieve correlatie. Dat laatste is het geval in ons voorbeeld: hogere sprinttijden horen gemiddeld genomen bij lagere sprongafstanden. Als r=0, dan is er geen correlatie, geen statistisch verband. En als r meer naar de 1 toekruipt, dan wordt het statistisch verband steeds sterker. Bij r=0,5 is het een matig verband, bij 0,75 een sterk verband, en bij 0,9 een zeer sterk verband. Tussen 0,3 en 0,5 is het verband zwak, en daaronder is er geen verband. b. Hoe kwalificeer je de sterkte van het verband tussen sprint-tijd en sprong-afstand     van deze groep kinderen? c. Doe hetzelfde voor het verband tussen vérgooien en vérspringen.     En ook voor vérgooien en sprint.     Kun je een verklaring bedenken waarom één van de statistische verbanden veel sterker is     dan de andere twee? d. Hoeveel meter voorspel je dat een kind zal gooien waarvan je weet dat het 4 meter vér springt?