| Uitwerkingen van H2D. | |
| 2.a. | Maak een staafdiagram voor de variabele klasse. De derde klasse is zowel absoluut als relatief de grootste klasse. Misschien heb je wel een vermoeden gezien de sociale situatie, maar door het ontbreken van data daarover zou een uitspraak speculatief zijn. |
| 2.b. | Maak een staafdiagram voor de variabele geslacht. Zowel absoluut als relatief zijn de mannen de meerderheid. Maak een staafdiagram met de variabele klasse. Groepeer op de variabele geslacht. Neem de bovenste van de drie soorten weergave. In alle drie klassen zijn de mannen in de meerderheid. Ook als percentage. |
| 2.c. | Er zijn drie babies van nog geen jaar. De jongste is dus niet bekend. Sorteer de variabele "leeftijd" van klein naar groot. Er zijn nogal wat leeftijden onbekend. Van degenen van wie de leeftijd wel bekend is is Johan Svensson de oudste, 74 jaar. |
| 2.d. | De vorm van het diagram laat zien dat er weinig kinderen onder de passagiers zijn. Het aantal jonge volwassen mensen is groot. Met de leeftijd nemen de aantallen geleidelijk af. |
| 2.e. |
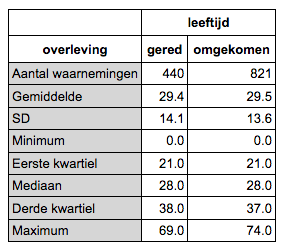
|
| 2.f. | Bijvoorbeeld zó: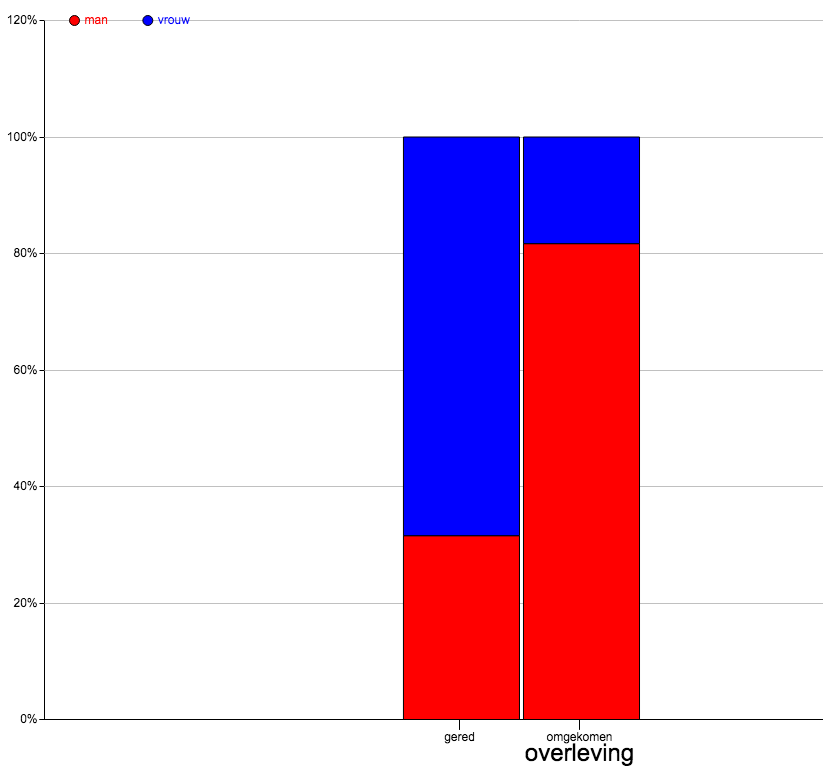
|
| 2.g. |
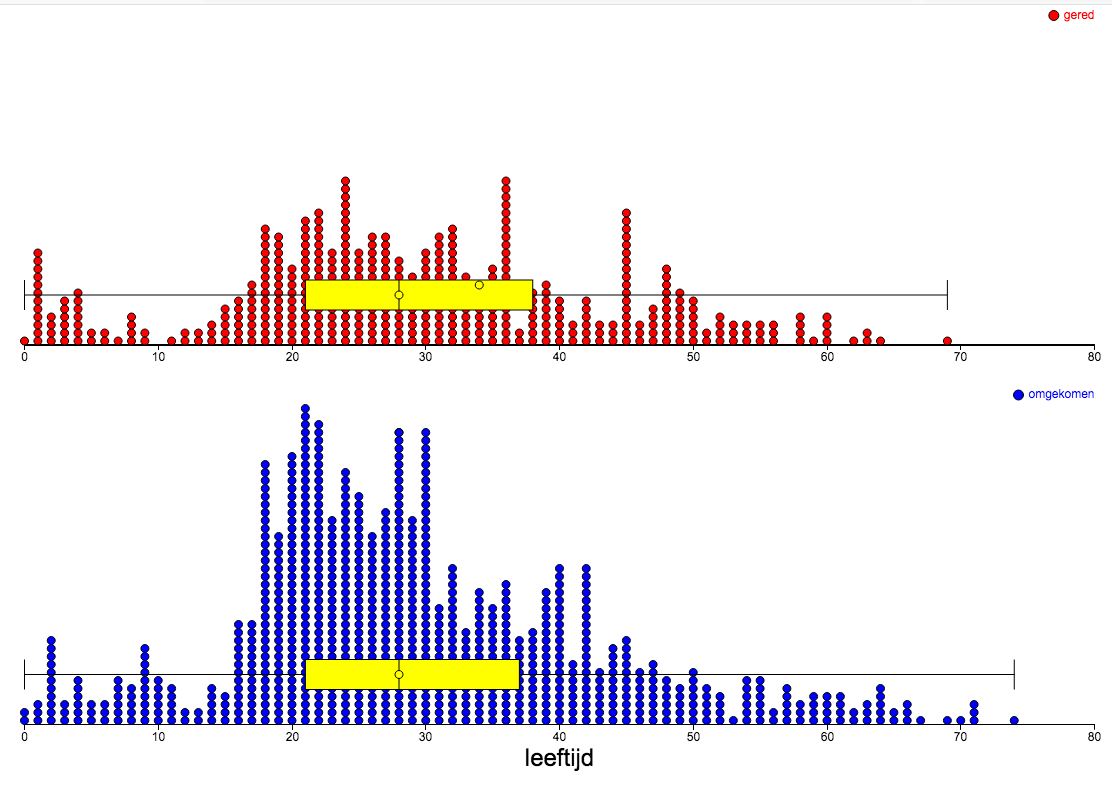
|
| 2.h. |
 Zo te zien: weinig verschil. |
| 2.i. |
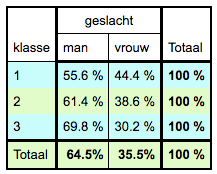 Hoe lager de klasse, hoe kleiner percentage vrouwen. Hoe lager de klasse, hoe kleiner percentage vrouwen.
|
| 2.j. |
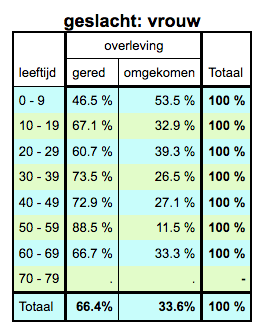 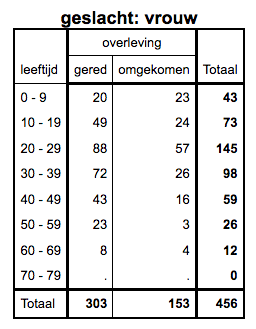 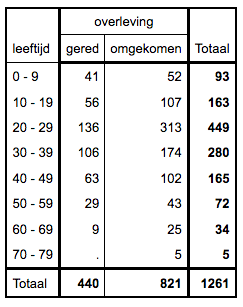 Percentueel de meeste 50-jarige vrouwen gered. In absolute aantallen de meeste twintig-jarige vrouwen gered EN omgekomen. Dat geldt trouwens ook voor de 20-jarige mensen. |
| 3.a. |
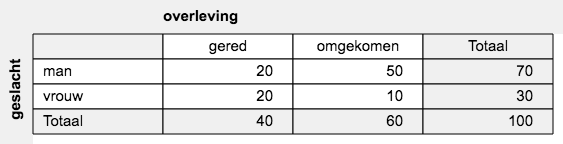
|
| 3.b. |
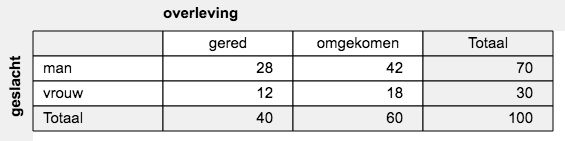 |
| 3.c. |
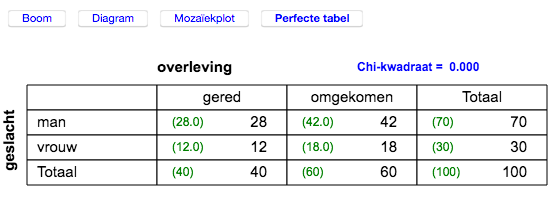 χ2 is een maat voor het verschil tussen de waargenomen tabel en de perfecte tabel. Die tabellen zijn hier hetzelfde. Het verschil is dus nul. Dus is ook Cramèrs V = 0. Om Cramèrs V op 0,5 te krijgen moet χ2 (in een 2x2 tabel met n = 100) gelijk zijn aan 5. |
| 3.d. |
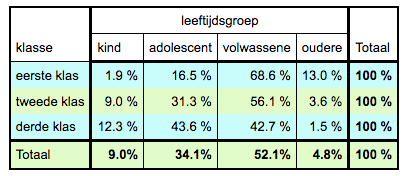 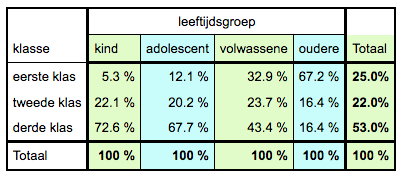 Zelf bedenken wat je opvalt.   Zelf bedenken wat je opvalt. 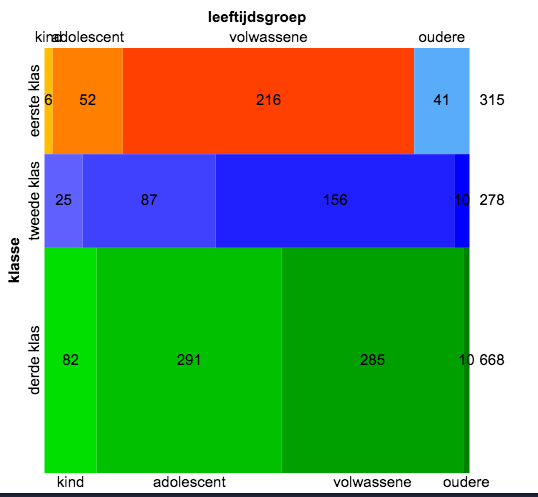 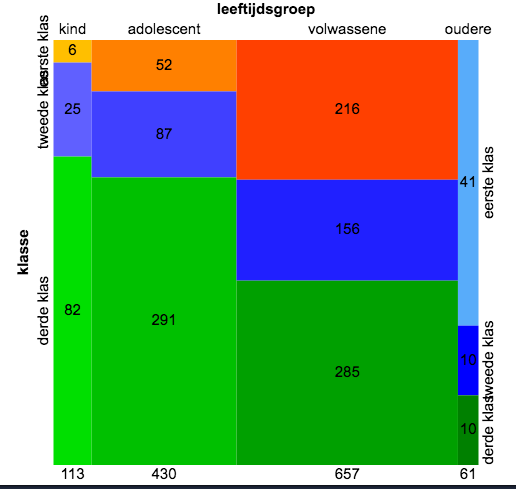 Zelf bedenken wat je opvalt. 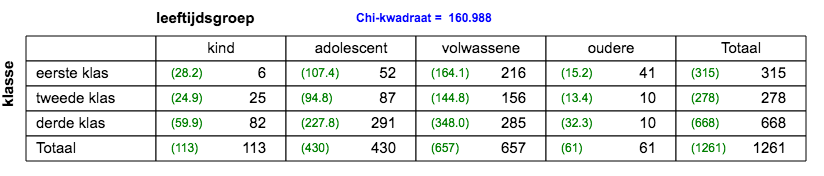 V = √(161/2*100) = 0,897. Er is een overduidelijk verband. |
| 3.e. |
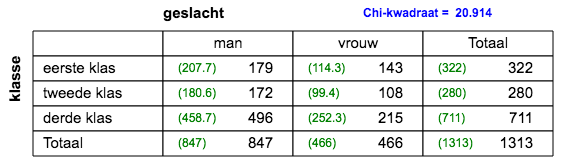 3x2 tabel; k=1; n=1313; V=0,13; zwak verband. 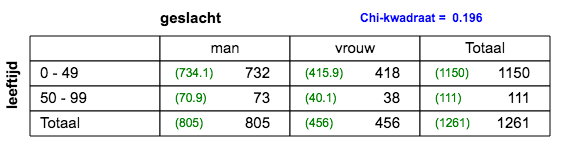 2x2 tabel; k=1; n=1261; V=0,01; er is geen verband. 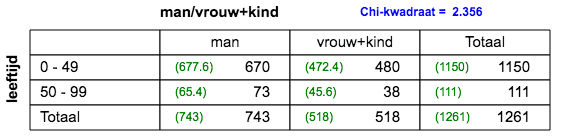 2x2 tabel; k=1; n=1261; V=0,04; er is geen verband. 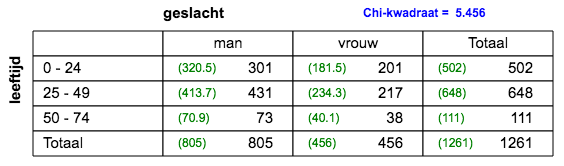 3x2 tabel; k=1; n=1261; V=0,07; er is geen verband. 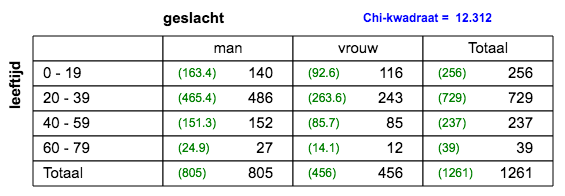 4x2 tabel; k=1; n=1261; V=0,01; zwak verband. |
| 4.a. |
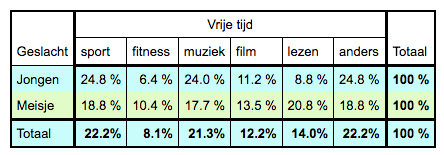 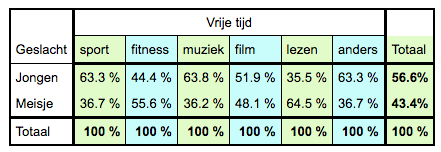 Zelf bedenken wat je opvalt.  2x6 tabel; er is misschien een verband. |
| 4.b. |
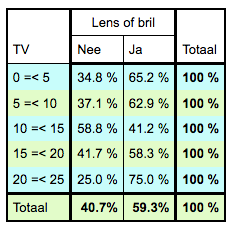 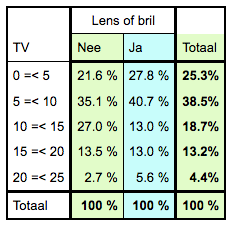 Zelf bedenken wat je opvalt. 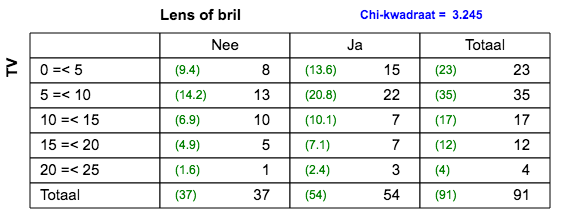 2x5 tabel; er is geen verband. |
| 4.c. |
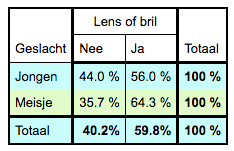 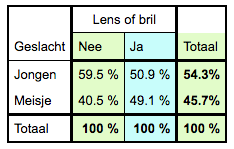 56% van de jongens draagt een bril/lens; 51% van de bril/lens-dragers is jongen. 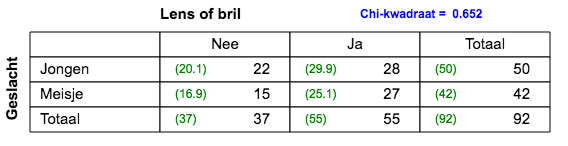 2x2 tabel; er is geen verband. |
| 4.d. |
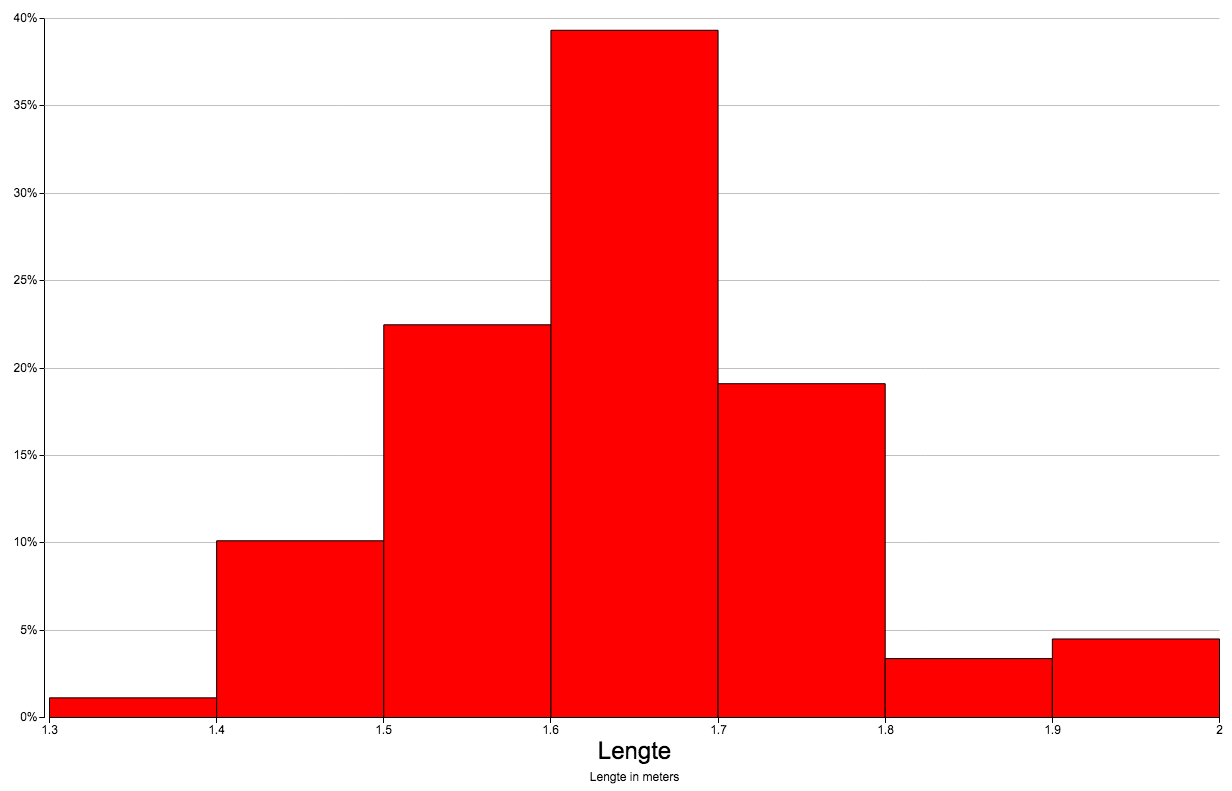 tussen 1,70 en 1,80: 39%; korter dan 1,70: 39+22,5+10+1=72,5%. 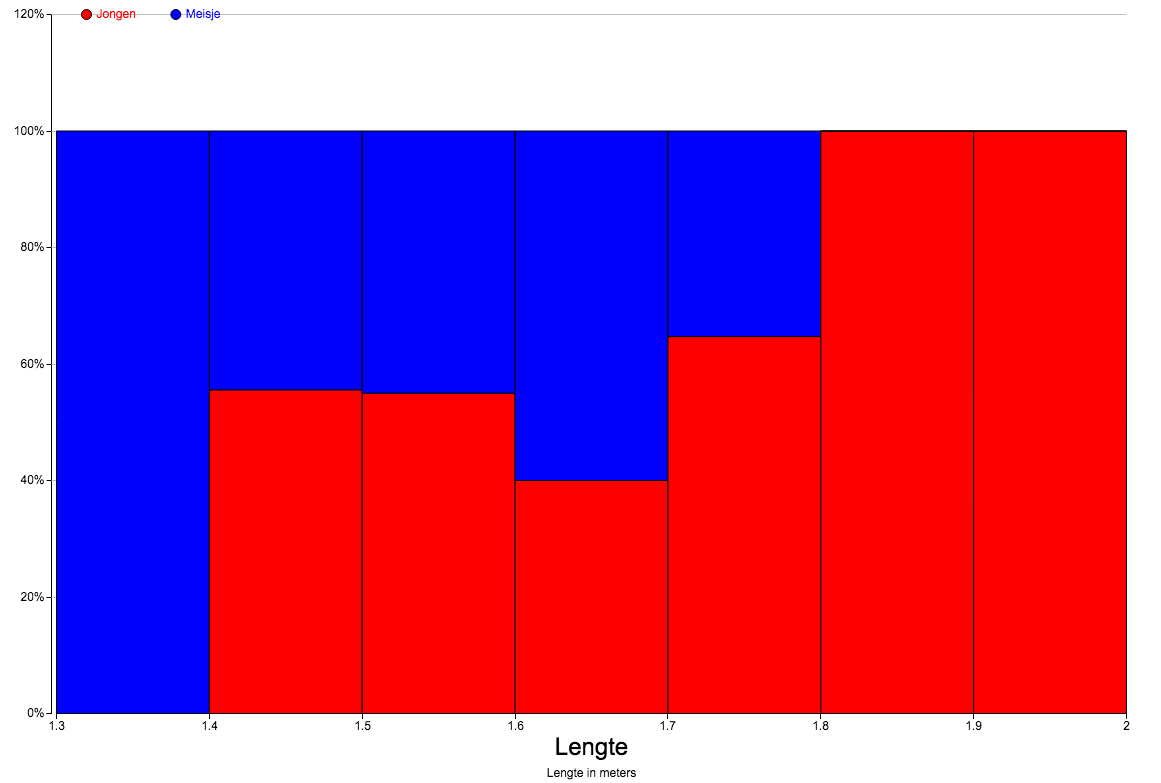 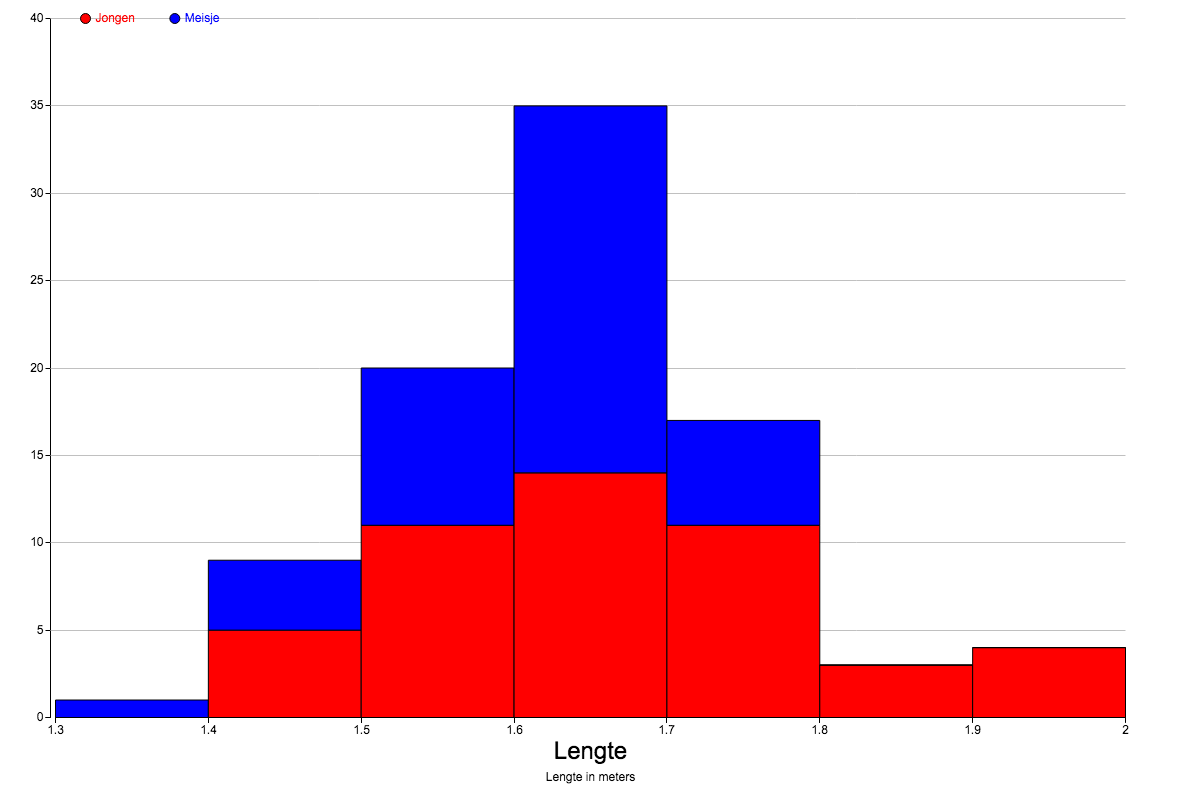 Bijvoorbeeld: geen hele korte jongens, geen lange meisjes; tussen 1,40 en 1,60 fifty-fifty; tussen 1,60 en 1,70 zijn de meisjes in de meerderheid. |
| 5.a. |
 2x4 tabel; er is misschien een verband. |
| 5.b. |
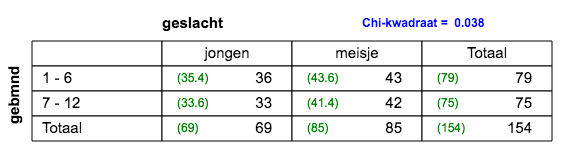 2x4 tabel; er is geen verband. |
| 5.c. |
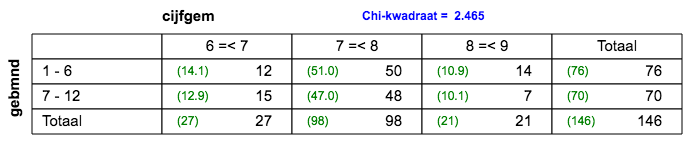 2x3 tabel; er is een verband. |
| 5.d. |
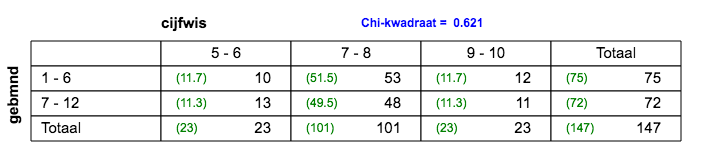 2x3 tabel; er is geen verband. |
| 5.e. |
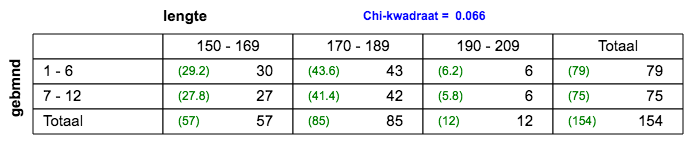 2x3 tabel; er is geen verband. |
| 5.f. |
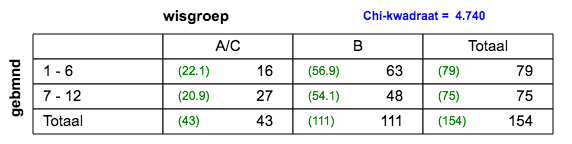 2x2 tabel; er is een verband. |
| 5.g. |
 2x6 tabel; er is een sterk verband. |
| 6.a. |
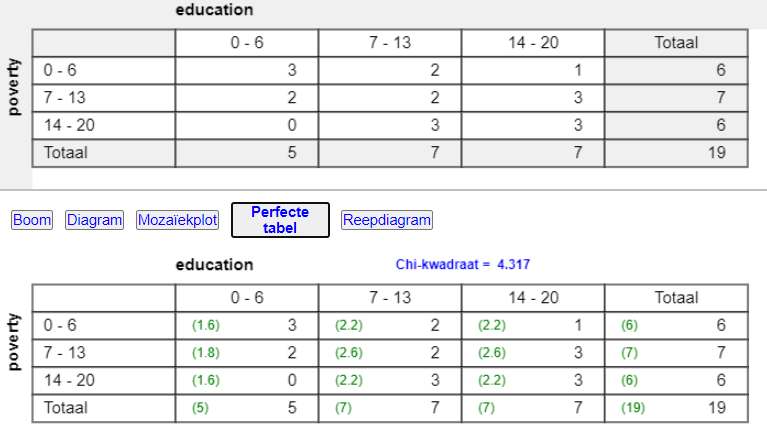 3x3 tabel; V = √ 4,317/(19·2) = 0,34; redelijk verband. |
| 6.b. |
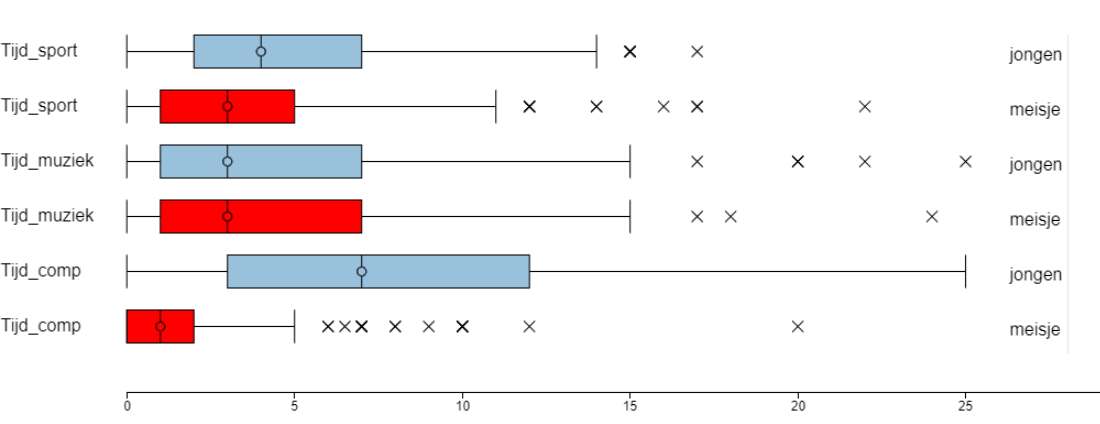 Het verschil bij sport is klein.; bij muziek is het nul; bij computers is het groot. |
| 6.c. |
- gemiddeld rapportcijfer: geen verschil voor j/m - gemiddeld rapportcijfer: matig verschil voor wisk AC/wisk B - wiskundecijfer: het valt op dat december afwijkt; er is matig verschil met de andere maanden, behalve met april/mei - wiskundecijfer: geen verschil; alleen de medianen verschillen - huiswerktijd: matig verschil voor j/m - gemiddeld rapportcijfer: zie hieronder: 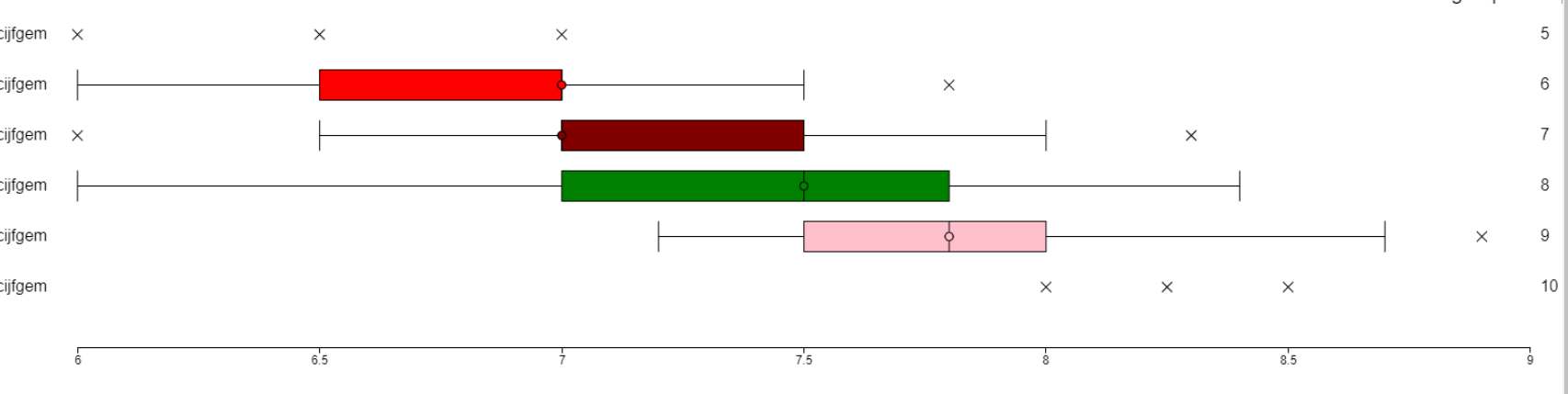 groot verschil in gemiddelde rapportcijfer tussen de leerlingen met een 6 en met een 9 voor wiskunde; iets minder groot verschil tussen de leerlingen met een 6 en met een 7 of 8 voor wiskunde; iets minder groot verschil tussen de leerlingen met een 7 en met een 9 voor wiskunde; geen verschil tussen de leerlingen met een 7 en met een 7 voor wiskunde - eigenlijk geen verschil in gemiddelde rapportcijfer voor wat betreft het aantal huiswerkuren; opvallend vind ik dat een "beetje huiswerk" hoort bij laag rapportcijfer en "heel weinig huiswerk" hoort bij een hoger rapportcijfer! 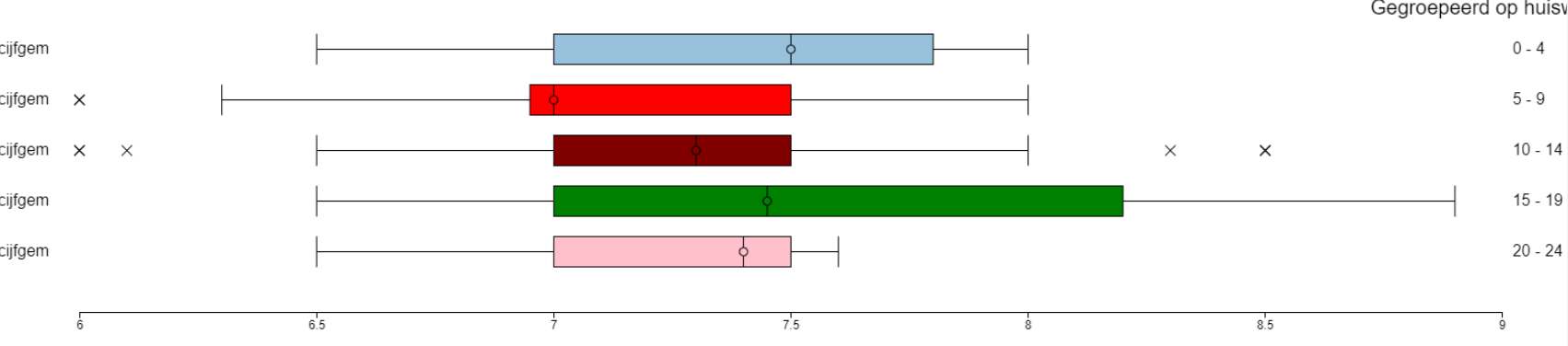 |

copyright